Question

A group of students at a high school took a standardized test. The number of students who

passed or failed the exam is broken down by class year in the following table. Determine
whether class year and passing the test are independent by filling out the blanks in the
sentence below. Write your answers as a decimal and round all probabilities to the
nearest hundredth.
Passed
12
27
Underclassman Upperclassman Total
15
20
16 36
35
28 63
Failed
Total
Since P(Passed) =
and P(Passed Underclassman) =
, the two results are
(write equal or not equal) so these events are
(write independent or not independent)
Activate

Answer 1

The table is attached.

Answer:

Since P(Passed) = 0.43, and P(Passed Underclassman) = 0.43, the two results are equal so these events are independent.

Explanation:

◙ From the table, we can see the probability of students who passed will be:

`P(passed) = (27)/(63) = (3)/(7)`

Converting to decimal, we have:

P(passed) = 0.42857 ≈ 0.43

◙Probability of students who failed:

`P(failed) = (36)/(63) = (4)/(7)`

Converting to decimal, we have:

P(failed) = 0.57142 ≈ 0.57

◙ P(passed upperclassman) =

`(12)/(28) = (3)/(7)`

Converting to decimal, we have:

P(passed upperclassman) = 0.42857 ≈ 0.43

◙P(failed upperclassman) =

`(16)/(28) = (4)/(7)`

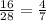
Converting to decimal, we have:

P(failed upperclassman) = 0.5714 ≈ 0.57

◙P(passed underclassman )
`= (15)/(35) = (3)/(7)`

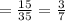
Converting to decimal, we have:

P(passed underclassman) = 0.42857 ≈ 0.43

◙ P(failed underclassman)

`= (20)/(35) = (4)/(7)`

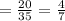
Converting to decimal, we have:

P(failed underclassman) = 0.5714 ≈ 0.57

Since P(Passed) = 0.43, and P(Passed Underclassman) = 0.43, the two results are equal so these events are independent.

Answer 2

Answer: provided in the explanation section

Explanation:

This is quite simple to analyze.

we have that:

• P (passed ) = 27/63 = 3/7

• P (passed/Underclassman ) = 15 / 35 = 3/7

• Since P (passed) = P(passed/underclassman) = 3/7

⇒ The two events are equal, hence independent.

cheers i hope this helped!!!!1