Answer:
a)
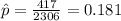
b)
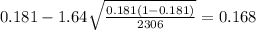
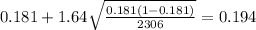
The 90% confidence interval would be given by (0.168;0.194)
c) For this case we are 90% confident that the true proportion of adult Americans aged 18 and older conducted by Harris Interactive found that 417 have donated blood in the past two years is between 0.168 and 0.194
d)
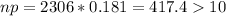
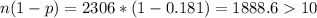
So then we satisfy all the requirements in order to assume the normal distribution for the parameter of interest
1. Yes, the requirements for constructing a confidence interval are satisfied.
Explanation:
Part a
For this case the point of estimate for the population proportion of adult Americans aged 18 and older who have donated blood in the past two years is given by:
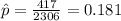
Part b
The confidence 90%, our significance level would be given by
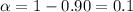 and
and
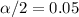 . And the critical value would be given by:
. And the critical value would be given by:
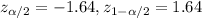
The confidence interval for the mean is given by the following formula:
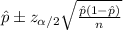
Replacing the info given we got:
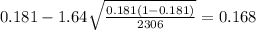
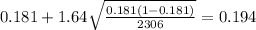
The 90% confidence interval would be given by (0.168;0.194)
Part c
For this case we are 90% confident that the true proportion of adult Americans aged 18 and older conducted by Harris Interactive found that 417 have donated blood in the past two years is between 0.168 and 0.194
Part d
For this case we need to satisfy:
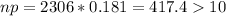
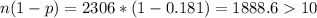
So then we satisfy all the requirements in order to assume the normal distribution for the parameter of interest
1. Yes, the requirements for constructing a confidence interval are satisfied.