Question

The diagram represents the enlargement of a rectangle by using a scale factor of 6.

A rectangle has a length of 30 feet and width of 6 feet.


What are the dimensions of the original rectangle?
5 feet by 1 foot
5 feet by 6 feet
25 feet by 1 foot
180 feet by 36 feet

Answer 1

Please consider the attached file.

We can see from attachment that sides of original rectangle are smaller than sides of new rectangle.

The new rectangle has a length of 30 feet and width of 6 feet.

To find the the length of original rectangle, we will divide sides of new rectangle by scale factor (6).

`\text{Length of original rectangle}=\frac{30\text{ ft}}{6}`

`\text{Length of original rectangle}=5\text{ ft}`

`\text{Width of original rectangle}=\frac{6\text{ ft}}{6}`

`\text{Width of original rectangle}=1\text{ ft}`

Therefore, the dimensions of original rectangle are 5 feet by 1 foot and option A is the correct choice.

Answer 2

The dimensions of the original rectangle are 5 feet by 1 foot

Explanation:

Let the x be the original length

let y be the original breadth

We are given that the enlargement of a rectangle by using a scale factor of 6.

So, Enlarged length = 6x

Enlarged breadth = 6y

We are given that A rectangle has a length of 30 feet and width of 6 feet.

Enlarged length = 6x = 30

`x=(30)/(6)`

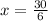
x=5

Enlarged breadth = 6y=6

`y=(6)/(6)`

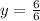
y=1

Hence the dimensions of the original rectangle are 5 feet by 1 foot