Question

The quadratic equation y=-0.5x+4x+10 models the path of a heavy ball through the air, where y represents the height in feet and x represents time in seconds. When will the ball hit the ground?

Answer 1

We have been given that the quadratic equation
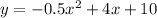`y=-0.5x^2+4x+10` models the path of a heavy ball through the air, where y represents the height in feet and x represents time in seconds. We are asked to find the time when ball will hit the ground.

The ball will hit the ground, when height of ball above ground will be 0. So we will equate our given quadratic equation with 0 and solve for x.

`-0.5x^2+4x+10=0`

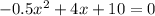
We will use quadratic formula to solve our given problem.

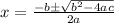`x=(-b\pm√(b^2-4ac))/(2a)`, where

b = Coefficient of x term,

a = Coefficient of
`x^2` term,

c = Constant.

`x=(-4\pm√((-4)^2-4(-0.5)(10)))/(2(-0.5))`

`x=(-4\pm√((16+20))/(-1)`

`x=(-4\pm√(36))/(-1)`

`x=(-4\pm6)/(-1)`

`x=(-4+6)/(-1), x=(-4-6)/(-1)`

`x=(2)/(-1), x=(-10)/(-1)`

`x=-2,x=10`

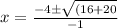
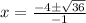
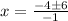
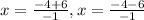
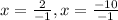
Since time cannot be negative, therefore, the ball will hit the ground after 10 seconds.