Question

The area of Rectangle A is twice the area of Rectangle B. The perimeter of Rectangle A is 20 units greater than the perimeter of Rectangle B. What could the dimensions of the two rectangles be?

Answer 1

One possible dimensions is: If Rectangle B is 1x2 then Rectangle A is 0.315x12.685

Explanation:

length of Rectangle A: a

width of Rectangle A: b

length of Rectangle B: c

width of Rectangle B: d

area of Rectangle A: a*b

area of Rectangle B: c*d

The area of Rectangle A is twice the area of Rectangle B:

2*c*d = a*b (eq. 1)

perimeter of Rectangle A: 2a + 2b

perimeter of Rectangle B: 2c + 2d

The perimeter of Rectangle A is 20 units greater than the perimeter of Rectangle B:

20 + 2c + 2d = 2a + 2b (eq. 2)

We have 4 variables (a, b, c and d) but only 2 equations, so we need to fix 2 variables and calculated the other ones. In this way, one of the infinite solutions is obtained. Selecting: c = 1 and d = 2, we get:

4 = a*b

26 = 2a + 2b

26b = 2a*b + 2b²

0 = 2b² -26b + 8

`b = (26 \pm √((-26)^2 - 4(2)(8)))/(2(2))`

`b = (26 \pm 24.739)/(4)`

`b_1 = (26 + 24.739)/(4)`

`b_1 = 12.685`

`b_2 = (26 - 24.739)/(4)`

`b_2 = 0.315`

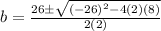
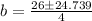
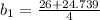
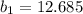
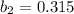
with b = 12.685, a = 4/12.685 = 0.315

with b = 0.315, a = 4/0.315 = 12.685