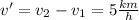Question

Two trains on parallel tracks are traveling in the same direction. One train starts 10 km behind the other. It overtakes the first train in 2 hours . What is the relative speed of the second train with respect to the first train?

Answer 1

`v'=v_2-v_1=5(km)/(h)`

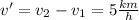
Step-by-step explanation:

The relative speed between the trains is given by:

`v'=v_2-v_1`

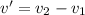
v1: speed of the first train

v2: speed of the second train

To find the relative velocity you write the equation of motion of both train by taking into account the information of the statement. The trains have constant velocity. Furthermore, the second train stars 10 km behind the other one. hence you have:

`x=10+v_1t\\\\x=v_2t`

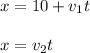
for t = 2 hours, the positions of both trains are equal, thus you have:

`10+v_1t=v_2t`

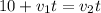
you factor v2 - v1 from the last equation and replace t = 2h:

`10=v_2t-v_1t\\\\10=(v_2-v_1)t\\\\v_2-v_1=(10)/(t)=(10)/(2)=5 (km)/(h)`

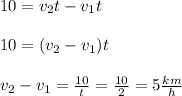
Hence, you have that the relative velocity is:

`v'=v_2-v_1=5(km)/(h)`