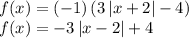Question

The graph of f(x) = |x| is vertically stretched by a factor of 3, shifted left 2 units, shifted down 4 units and reflected over the x-axis. What is the function equation of the resulting graph?

Answer 1

The final transformed function becomes:

`f(x)=-3\,|x-2|+4`

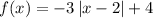
Explanation:

The first transformation (vertically stretched by a factor of 3) means we multiply by 3 the original function:

`f(x)= 3\,|x|`

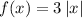
second transformation (shifted left 2 units) means we add 2 units to "x":

`f(x)=3\,|x+2|`

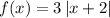
third transformation (shifted down 4 units) implies that we subtract 4 units to the full functional expression:

`f(x)=3\,|x+2|-4`

fourth transformation (reflected over the x-axis) implies that we multiply the full functional expression by "-1":

`f(x)=(-1)\,(3\,|x+2|-4)\\f(x)=-3\,|x-2|+4`

Answer 2

Explanation:

Step 1: Add the vertical stretch

`f(x) = |x|`

`f(x) = 3|x|`

Step 2: Shift it to the left 2 units

`f(x) = 3|x|`

`f(x) = 3|x + 2|`

Step 3: Shift it down 4 units

`f(x) = 3|x + 2|`

`f(x) = 3|x + 2| - 4`

Step 4: Reflect it across the x-axis

`f(x) = 3|x + 2| - 4`

`f(x) = -3|x + 2| - 4`

Answer:
`f(x) = -3|x + 2| - 4`