Question

A first order reaction has rate constants of 4.6 x 10-2 s-1 and 8.1 x 10-2 s-1 at 0ºC and 20ºC, respectively. What is the value for the activation energy?

A.
0.566 J/mol
B.
2.5 x 10-4 J/mol
C.
2260 J/mol
D.
18,800 J/mol
E.
1.76 J/mol

Answer 1

D. 18,800 J/mol

Step-by-step explanation:

We need to use the Arrhenius equation to solve for this problem:

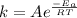`k=Ae^{(-E_a)/(RT)`, where k is the rate constant, A is the frequency factor,
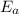`E_a` is the activation energy, R is the gas constant, and T is the temperature in Kelvins.

We want to find the value of
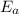`E_a`, so let's plug some of the information we have into the equation. The gas constant we can use here is 8.31 J/mol-K.

At 0°C, which is 0 + 273 = 273 Kelvins, the rate constant k is
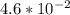`4.6*10^(-2)`. So:

`k=Ae^{(-E_a)/(RT)`

`4.6*10^(-2)=Ae^{(-E_a)/(8.31*273)`

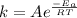
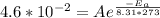
At 20°C, which is 20 + 273 = 293 Kelvins, the rate constant k is
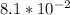`8.1*10^(-2)`. So:

`k=Ae^{(-E_a)/(RT)`

`8.1*10^(-2)=Ae^{(-E_a)/(8.31*293)`

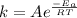
We now have two equations and two variables to solve for. We just want to find Ea, so let's write the first equation for A in terms of Ea:

`4.6*10^(-2)=Ae^{(-E_a)/(8.31*273)`

`A=\frac{4.6*10^(-2)}{e^{(-E_a)/(8.31*273)} }`

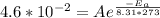
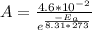
Plug this in for A in the second equation:

`8.1*10^(-2)=Ae^{(-E_a)/(8.31*293)`

`8.1*10^(-2)=\frac{4.6*10^(-2)}{e^{(-E_a)/(8.31*273)} }e^{(-E_a)/(8.31*293)`

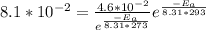
After some troublesome manipulation, the answer should come down to be approximately:

Ea = 18,800 J/mol

The answer is thus D.