Question

A basket contains 10 plastic eggs, each with a coin. There are 4 pennies, 3 nickels, 2 dimes, and 1 quarter. Tim picks two eggs randomly from the basket. What do the probabilities of one egg containing a nickel and one egg containing a quarter show about the independence or dependence of the events?

a
The events are dependent because P(Q)⋅P(N|Q)≠P(N)⋅P(Q|N).
b
The events are independent because P(Q)⋅P(N|Q)≠P(N)⋅P(Q|N).
c
The events are dependent because P(Q)⋅P(N|Q)=P(N)⋅P(Q|N).
d
The events are independent because P(Q)⋅P(N|Q)=P(N)⋅P(Q|N).

Answer 1

The correct option is a: The events are dependent because P(Q)⋅P(N|Q)≠P(N)⋅P(Q|N)

Explanation:

These events are dependent events since picking out an egg containing a nickel will affect the probability of picking out an egg containing a quarter (or any other of the type of coins given in the statement, for that matter). Getting a nickel on the first pick has a probability of
`(3)/(10)` and a getting a quarter on the second pick has a probability of
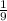`(1)/(9)`. The probability of both events happening is not equal to the product of each event happening individually.

Hope that answers the question, have a great day!