Question

A person with normal vision can focus on objects as close as a few centimeters from the eye up to objects infinitely far away. There exist, however, certain conditions under which the range of vision is not so extended. For example, a nearsighted person cannot focus on objects farther than a certain point (the far point), while a farsighted person cannot focus on objects closer than a certain point (the near point). Note that even though the presence of a near point is common to everyone, a farsighted person has a near point that is much farther from the eye than the near point of a person with normal vision.

Both nearsightedness and farsightedness can be corrected with the use of glasses or contact lenses. In this case, the eye converges the light coming from the image formed by the corrective lens rather than from the object itself.If a nearsighted person has a far point df that is 3.50 m from the eye, what is the focal length f1 of the contact lenses that the person would need to see an object at infinity clearly?

Answer 1

Step-by-step explanation:

For a person suffering from nearsightedness, far point is 3.5 m . That means , an object beyond 3.5 m will not be clearly visible by the person . Ray of light coming from 3.5 m will be focussed on retina . For an object to be visible from infinity , ray of light coming from infinity should appear to be coming from 3.5 m . In other words , the object placed at infinity should form a virtual image at 3.5 m . This can be done by concave lens.

u = ∝ ; v = 3.5

Using lens formula

`(1)/(v) -(1)/(u) = (1)/(f)`

`(1)/(-3.5) -0 = (1)/(f)`

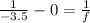
f = - 3.5 m .