Question

Which equation represents circle q

Answer 1

We have been given an image of circle Q. We are asked to find the equation of the circle.

We know that standard form of circle is
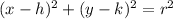`(x-h)^2+(y-k)^2=r^2`, where point (h,k) represents center of circle and r represents radius of circle.

We can see that center of circle is at point (11,3).

We will find radius of circle using distance formula between center and point on circle as:

`r=√((11-(-4))^2+(3-7)^2)`

`r=√((11+4)^2+(-4)^2)`

`r=√((15)^2+16)`

`r=√(225+16)`

`r=√(241)`

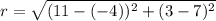
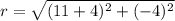
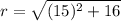
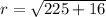
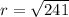
Upon substituting our given values in equation of circle, we will get:

`(x-11)^2+(y-3)^2=(√(241))^2`

`(x-11)^2+(y-3)^2=241`

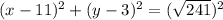
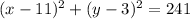
Therefore, our required equation would be
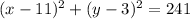`(x-11)^2+(y-3)^2=241` and option A is the correct choice.