Question

I need a hand with this one

Answer 1

x = 9

Explanation:

2(x+5)-7=3(x-2)

x = 9

Answer 2

`x=9`

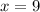
Explanation:

First Let's rewrite the equation.

`2(x+5)-7=3(x-2)`

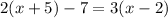
Now lets simplify.

We will start by distributing.

`(2)(x)+(2)(5)+(-7)=(3)(x)+(3)(-2)`

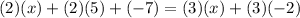
That will now look like:

`2x+10+(-7)=3x+(-6)`

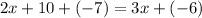
Now we will simplify even further.

To do so we must combine like terms!

`(2x)+(10+(-7))=3x(-6)`

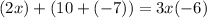
10 plus negative 7 is equal to 3.

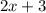`2x + 3` is the first part of our equation.

Now we will want to isolate the x values.

To do so we will want to subtract 3 from both sides.

-6 minus 3 is equal to -9

Our new equation is

`2x=3x-9`

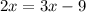
Now we will subtract 3x from both sides.

2x-3x= -x

Our new equation is:

`-x=-9`

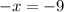
Now we will divide both sides by 1, this way both sides will be positive.

`(-x)/(1) =(-9)/(1)`

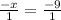
That equals:

`x=9`

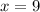
Thus, Our answer is
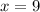`x=9`!