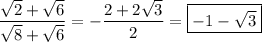The trick is to exploit the difference of squares formula,
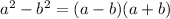
Set a = √8 and b = √6, so that a + b is the expression in the denominator. Multiply by its conjugate a - b:
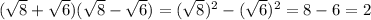
Whatever you do to the denominator, you have to do to the numerator too. So
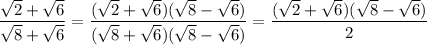
Expand the numerator:
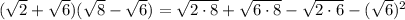
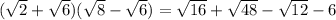
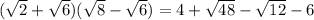
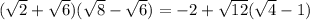
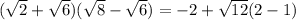
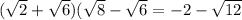
So we have
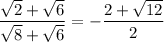
But √12 = √(3•4) = 2√3, so