Answer:
The radius of the base of the small cone is 3 feet
Explanation:
The question requires the determination of the radius of the smaller cone
Therefore, height of the larger cone = 10 feet
Base diameter of the larger cone = 10 feet
Height of horizontal plane of small plane above base of larger cone = 4 feet
Hence the height of the small cone = 6 feet
Therefore, by similar triangles, and tangents we have;
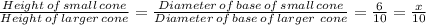
Where:
x = The diameter of the base of the small cone
Therefore;
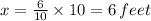
The radius of the base of the small cone = half the diameter of the base of the small cone
∴ The radius of the base of the small cone = (6 feet)/2 = 3 feet.