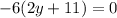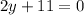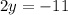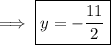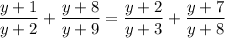
Write all fractions in terms of a common denominator:
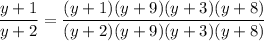
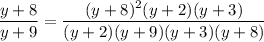
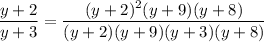
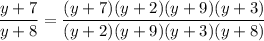
Then move all fractions to one side and simplify the numerator:
![((y+1)(y+9)(y+3)(y+8)+(y+8)^2(y+2)(y+3)-(y+2)^2(y+9)(y+8)-(y+7)(y+2)(y+9)(y+3))/((y+2)(y+9)(y+3)(y+8))=0]()
The numerator dictates when the fraction reduces to 0. The denominator can never be 0, so we know that y cannot take any of the values -2, -9, -3, nor -8.
So the equation reduces to
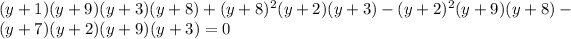
Expand the left side; you would end up with