Answer:
width = 16 cm
length = 19 cm
Explanation:
Let the width be x cm.
Given that length is 3 cm more than width then
length = x+3 cm
area of rectangle = 304 square cm. -----1
area of rectangle is given by
area =length * width
substituting from equation 1 and length and width in terms of x we have
304 = x(x+3)
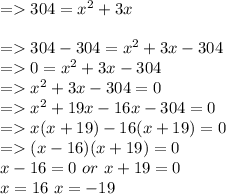
As length cannot be negative hence x = 16
Thus width = x = 16 cm
length = x+3 = 16+3 = 19 cm