Answer:
The confidence interval for the true mean is given by the following formula:
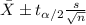 (1)
(1)
The confidence interval for this case i given by:
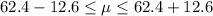
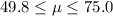
For this case we can conclude that the true mean for the time that students will require to complete a particular examination is between 49.8 and 75.0 minutes. And the best option for this case by:
A) We are 96% confident that the population mean time required for all students who take this test is somewhere between 49.8 and 75.0 minutes
Explanation:
The confidence interval for the true mean is given by the following formula:
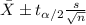 (1)
(1)
The confidence interval for this case i given by:
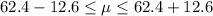
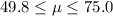
For this case we can conclude that the true mean for the time that students will require to complete a particular examination is between 49.8 and 75.0 minutes. And the best option for this case by:
A) We are 96% confident that the population mean time required for all students who take this test is somewhere between 49.8 and 75.0 minutes