Answer:
The number of miles biked each day by the bicyclists varied by an average of 4 miles from the mean.
Explanation:
The mean absolute deviation (MAD) of a data set is the average distance amid each value and the mean. The MAD provides us with an idea about the deviation in the data-set.
The formula to calculate the value of MAD is,
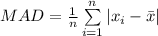
The data is:
S = {7, 10, 13, 4, 12, 21, 10, 3}
Compute the mean of the data as follows:
![\bar x=(1)/(n)\sum\limits^(n)_(i=1){x_(i)}\\\\=(1)/(8) [7+10+13+4+12+21+10+3]\\\\=10](https://img.qammunity.org/2021/formulas/mathematics/high-school/lbt9krut0t0cldz8ntw85ec4ujx5sxs69c.png)
Compute the value of MAD as follows:
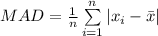
![=(1)/(8)* [|7-10|+|10-10|+|13-10|+...+|3-10|]\\\\=(32)/(8)\\\\=4](https://img.qammunity.org/2021/formulas/mathematics/high-school/fm0cnr9y1qpd90m93y0utmnm40mxjerckr.png)
Thus, the mean absolute deviation is 4.
The number of miles biked each day by the bicyclists varied by an average of 4 miles from the mean.