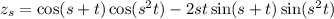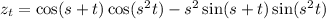1. By the chain rule,
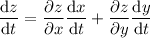
I'm going to switch up the notation to save space, so for example,
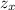 is shorthand for
is shorthand for
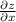 .
.
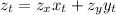
We have
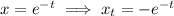
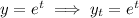
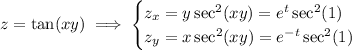
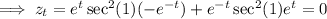
Similarly,
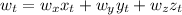
where
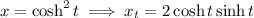
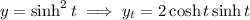

To capture all the partial derivatives of
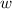 , compute its gradient:
, compute its gradient:
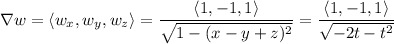
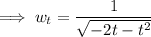
2. The problem is asking for
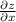 and
and
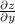 . But
. But
 is already a function of
is already a function of
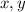 , so the chain rule isn't needed here. I suspect it's supposed to say "find
, so the chain rule isn't needed here. I suspect it's supposed to say "find
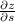 and
and
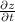 " instead.
" instead.
If that's the case, then
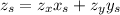
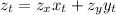
as the hint suggests. We have
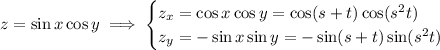
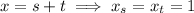
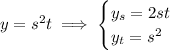
Putting everything together, we get