Question

Write the standard form of the equation of the circle that passes through the point

(0, 1) with its center at the origin.

Answer 1

The standard form of the equation of the circle is
`x^2+y^2=1`.

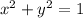Explanation:

A circle is the set of points in a plane that lie a fixed distance, called the radius, from any point, called the center.

The equation of a circle in standard form is

`(x-h)^2+(y-k)^2=r^2`

where r is the radius of the circle, and h, k are the coordinates of its center.

When the center of the circle coincides with the origin
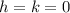`h=k=0`, so

`(x-0)^2+(y-0)^2=r^2\\x^2+y^2=r^2`

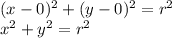
We are also told that the circle contains the point (0, 1), so we will use that information to find the radius r.

`0^2+1^2=r^2\\r^2=0^2+1^2\\r^2=1\\r=√(1)`

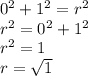
Therefore, the standard form of the equation of the circle is
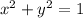`x^2+y^2=1`.