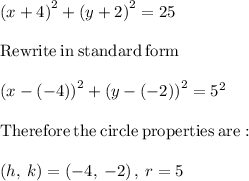Question

Write the equation in standard form and then find the center (h, k) and radius r of the circle. Be sure to show all answers.

x2+8x+y2+4y−5=0

Answer 1

The standard form equation is
`\left(x-\left(-4\right)\right)^2+\left(y-\left(-2\right)\right)^2=5^2`.

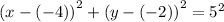The center is
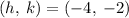`\left(h,\:k\right)=\left(-4,\:-2\right)` and the radius is
`r=5`.

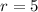Explanation:

The standard form of an equation of a circle is
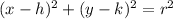`(x-h)^2+(y-k)^2=r^2` where
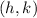`(h,k)` is the center and the radius is
`r`.

To write the equation
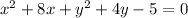`x^2+8x+y^2+4y-5=0` in the form of the standard circle equation you must:

`\mathrm{Move\:the\:five\:to\:the\:right\:side} \\\\x^2+8x+y^2+4y=5\\\\\mathrm{Group\:x-variables\:and\:y-variables\:together}\\\\\left(x^2+8x\right)+\left(y^2+4y\right)=5\\\\\mathrm{Convert}\:x\:\mathrm{to\:square\:form}\\\\\left(x^2+8x+16\right)+\left(y^2+4y\right)=5+16\\\left(x+4\right)^2+\left(y^2+4y\right)=5+16\\\\\mathrm{Convert}\:y\:\mathrm{to\:square\:form}\\\\\left(x+4\right)^2+\left(y^2+4y+4\right)=5+16+4\\\left(x+4\right)^2+\left(y+2\right)^2=5+16+4\\`

`\left(x+4\right)^2+\left(y+2\right)^2=25\\\\\mathrm{Rewrite\:in\:standard\:form}\\\\\left(x-\left(-4\right)\right)^2+\left(y-\left(-2\right)\right)^2=5^2\\\\\mathrm{Therefore\:the\:circle\:properties\:are:}\\\\\left(h,\:k\right)=\left(-4,\:-2\right),\:r=5`