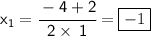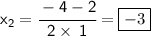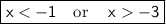Question

Solving quadratic inequalities

Answer 1

`\boxed{\sf x < -3\quad \mathrm{or}\quad \:x > -1}`

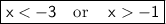
Explanation:

`\sf x^2+4x+3 > \:0`

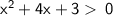
In order to solve inequality, we need to factor the left hand side. we can use the transformation
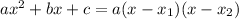`ax^2+bx+c=a(x-x_1)(x-x_2)` to factor quadratic polynomials. where x(1) & x(2) are the solutions of the quadratic equation ax²+bx+c=0 .

`\sf x^2+4x+3=0`

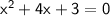
Quadratic formula:-

`\boxed{\sf x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)}`

`\sf a=1\\b=4\\c=3`

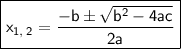
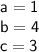
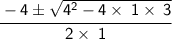`\sf \cfrac{-4\pm √(4^2-4* \:1* \:3)}{2* \:1}` ← Calculate

`\sf √(4^2-4* \:1* \:3)=\boxed{2}`

`\sf \cfrac{-4\pm \:2}{2* \:1}`

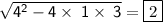
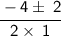
Now, let's Separate the solutions,

`\sf x_1=\cfrac{-4+2}{2* \:1},\:x_2=\cfrac{-4-2}{2* \:1}`

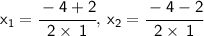
Do the calculations,

`\sf x_1=\cfrac{-4+2}{2* \:1}=\boxed{-1}`

`\sf x_2=\cfrac{-4-2}{2* \:1}=\boxed{-3}`

`\boxed{\sf x < -1\quad \mathrm{or}\quad \:x > -3}`