A: The center is the mid point of the diameter. So, the center of the circle will be the midpoint of points P and Q. The coordinates of the midpoint are the averaged coordinates of the endpoints.
So, the x-cooardinate of the center is the average of the x-coordinates of P and Q:
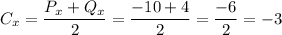
Try to do the same thing with the y coordinates, and you'll get the y-coordinate
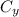 . This first part will be over, because the circle will be point
. This first part will be over, because the circle will be point
B: The radius is exactly half the diameter. So, we find the length of the diameter, and we divide it by 2. To find the length of the diameter, we use the standard formula for the distance between two points:
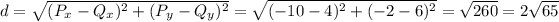
Divide this length by 2 and you'll get the radius.
C: At this point, we have both the radius and the coordinates of the center. The equation of the circle depends on these two parameters, and it is
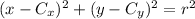
Substitute
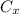 and
and
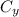 with the coordinates of the center (found in point A.) and
with the coordinates of the center (found in point A.) and
 with the radius (found in point B.) and you'll have the equation of the circle.
with the radius (found in point B.) and you'll have the equation of the circle.