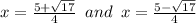Answer:
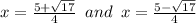
which agrees with the last two options in the list of possible answers
(mark both)
Explanation:
We start by re-writing the quadratic equation in standard form:
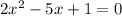
Which can be solved by using the quadratic formula for a quadratic
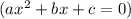
with parameters:
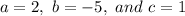
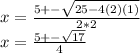
Therefore the two values are: