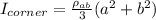Answer:
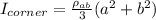
Explanation:
By applying the concept of calculus;
the moment of inertia of the lamina about one corner
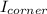 is:
is:
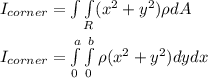
where :
(a and b are the length and the breath of the rectangle respectively )
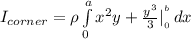
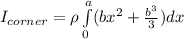
![I_(corner) = \rho [(bx^3)/(3)+ (b^3x)/(3)]^ {^ a} _(_0)](https://img.qammunity.org/2021/formulas/mathematics/college/6ua7xnblobuzyai1m1jpnovbp3ugdq9hbd.png)
![I_(corner) = \rho [(a^3b)/(3)+ (ab^3)/(3)]](https://img.qammunity.org/2021/formulas/mathematics/college/3gdor1ldoox50ye8sorqxue7oza1l87glc.png)
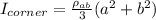
Thus; the moment of inertia of the lamina about one corner is