Answer:
The surface area of the box is equal to 214.76 cm².
The approximate cost of the velvet to cover the box is equal to $4.30.
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Geometry
Surface Area Formula [Rectangular Prism]:
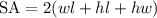
- w is width
- l is length
- h is height
Explanation:
Step 1: Define
Identify given.
h = 1.02 cm
l = 8 cm
w = 11 cm
Step 2: Find Surface Area
- [Surface Area Formula - Rectangular Prism] Substitute in variables:
![\displaystyle \text{SA} = 2 \bigg[ (11 \ \text{cm})(8 \ \text{cm}) + (1.02 \ \text{cm})(8 \ \text{cm}) + (1.02 \ \text{cm})(11 \ \text{cm}) \bigg]](https://img.qammunity.org/2021/formulas/mathematics/high-school/yksmepq6ihekuizdmkwdj2fg9e5eg7cuwg.png)
- Evaluate [Order of Operations]:
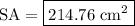
∴ the surface area of the small box is equal to 214.76 cm².
Step 3: Find Cost
To find the cost of covering the entire box, we can simply multiply the unit cost to the surface area to find out the net price:
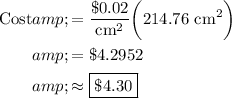
∴ the cost to cover the entire surface of the box is equal to approximately $4.30.
---
Topic: Geometry