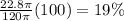Answer:
Percentage decrease in surface area =
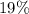
Explanation:
Given: A right circular cylinder has a radius of 6 inches and a height of 4 inches.
To find: percent change in surface area of the cylinder if height and radius are decreased by 10%
Solution:
Original radius of cylinder (r) = 6 inches
Original height of cylinder (h) = 4 inches
Original surface area of cylinder (a) =

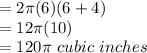
New radius of cylinder (R) =
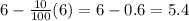 inches
inches
New height of cylinder (H) =
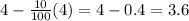
New surface area of cylinder (A) =
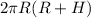
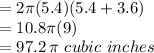
Decrease in surface area =
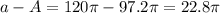
Percentage decrease in surface area =