Question

Determining a Quadratic Function with a

Which function has a vertex at (2, -9)?
f(x) = -(x-3)2
f(-x) = (x + 8)2
f(x) = (x - 5)(x + 1)
f(x) = -(x - 1)(x - 5)

Answer 1

Answer: f(x) = (x-5)(x+1)

Explanation:

a. f(x) = -(x-3)2

y = (-x+3)2

-9 = -2x+6

-15 = -2x

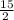`(15)/(2\\)` = x

x =
`(15)/(2)`

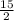
vertex at {
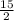`(15)/(2)`, -9} (wrong)

b. f(-x) = (x+8)2

-y = 2x+16

9 = 2x+16

9-16 = 2x

-7 = 2x

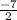`(-7)/(2)` = x

x =
`(-7)/(2)`

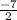
vertex at {
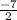`(-7)/(2)`, -9} (wrong)

c. f(x) = (x-5)(x+1)

y = (2-5)(2+1)

y = (-3)(3)

y = -9

vertex at {2, -9} (right)

d. f(x) = -(x-1)(x-5)

y = -(2-1)(2-5)

y = -(1)(-3)

y = 3

vertex at {2, 3} (wrong)