Question

Determine if \sqrt{41}

41
​
is rational or irrational and give a reason for your answer.

Answer 1

Assume √41 is rational, so that there exist integers p, q such that

`√(41) = \frac pq`

and p/q is irreducible. Taking squares, this would mean

`41 = (p^2)/(q^2) \implies p^2 = 41q^2`

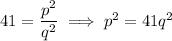
This tells us that 41 is a factor of p², which in turn means 41 is a factor of p because 41 is prime. We can consequently write p = 41n for some integer n. But then

`p^2 = (41n)^2=41q^2 \implies 41n^2 = q^2`

which says 41 also divides q² and hence divides q as well. In other words, p/q is reducible, so we have a contradiction.