Question

1.Suppose that scores on a knowledge test are normally distributed with a mean of 71 and a standard deviation of 6

A. Label the curve: show the mean and the value of each standard deviation


B. If Angelica scored a 76 on the test what is her Z score (draw her score on the curve above and label)


C. What percent of students did Angelica score higher than? How can you tell?


D. If 185 students took the test how many students scored higher than Angelica

Answer 1

a) For this case we can see the distribution in the figure attached is a bell shaped graph and symmetrical around 71

b)
`z = (76-71)/(6)= 0.833`

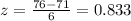
We can see the value of 76 labeled in the second picture attached

c)
`P(X>76)`

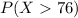
And using the z score we have this using the normal standard table or excel:

`P(Z>0.833) = 1-P(Z<0.833) = 0.202`

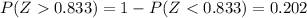
d)
`n = 185*0.202= 154.16`

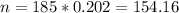
We can say that about 154 and 155 students scored higher than Angelica

Explanation:

We know that X represent the random variable scores of knowledge test and is given by:

`X \sim N (\mu = 71, \sigma =6)`

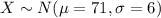
Part a

For this case we can see the distribution in the figure attached is a bell shaped graph and symmetrical around 71

Part b

For this case the z score is given by:

`z = (X- \mu)/(\sigma)`

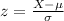
And replacing we got:

`z = (76-71)/(6)= 0.833`

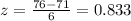
We can see the value of 76 labeled in the second picture attached

Part c

We want this probability:

`P(X>76)`

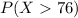
And using the z score we have this using the normal standard table or excel:

`P(Z>0.833) = 1-P(Z<0.833) = 0.202`

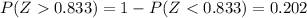
Part d

For this case we can find the number desired like this:

`n = 185*0.202= 154.16`

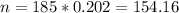
We can say that about 154 and 155 students scored higher than Angelica