Answer:
The answer is "Slope coefficient is significant".
Explanation:
Slope is = - 68565
By each unit, this same value of the response variable reduces by – 6.86 throughout the slope value obtained
Consider zero hypothesis and options
Zero assumptions,
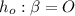
Hypothesis of alternative,
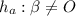
Suppose that now the degree of importance is= 0.05
The p-value of the slope coefficient estimates is =0.000
Compare the p-value and the meaning
That p-value is smaller than the meaning level and rejects the null hypothesis
That's why the slope coefficient value is therefore significant.