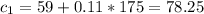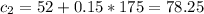Question

Omar will rent a car for the weekend. He can choose one of two plans. The first plan has an initial fee of $59 and costs an additional 50.11 per mile driven. The

second plan has an initial fee of $52 and costs an additional $0.15 per mile driven

For what amount of driving do the two plans cost the

What is the cost when the two plans cost the same?

Answer 1

`59 +0.11 x = 52 +0.15 x`

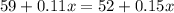
And solving for x we got:

`7= 0.04 x`

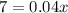
And replacing for x we got:

`x = (7)/(0.04)= 175`

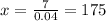
And for the cost would be:

`c_1 = 59 +0.11*175 = 78.25`

`c_2 = 52 +0.15*175 = 78.25`

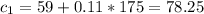
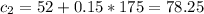
Explanation:

Assuming the following info corrected :Omar will rent a car for the weekend. He can choose one of two plans. The first plan has an initial fee of $59 and costs an additional 0.11 per mile driven. The second plan has an initial fee of $52 and costs an additional $0.15 per mile driven

For this case we know that the first plan has an initial fee of $59 and costs an additional 50.11 per mile driven and the second plan has an initial fee of $52 and costs an additional $0.15 per mile driven.

So we can set up the following equations for each cost

`c_1 = 59 +0.11 x`

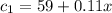
With c1 the cost of the plan 1 and x the number of miles

`c_2 = 52 +0.15 x`

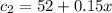
With c2 the cost of the plan 2 and x the number of miles

We can set equatl the two costs:

`c_1 = c_2`

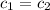
And replacing we got:

`59 +0.11 x = 52 +0.15 x`

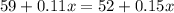
And solving for x we got:

`7= 0.04 x`

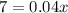
And replacing for x we got:

`x = (7)/(0.04)= 175`

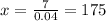
And for the cost would be:

`c_1 = 59 +0.11*175 = 78.25`

`c_2 = 52 +0.15*175 = 78.25`