Question:
What is the area of the sector? Either enter an exact answer in terms of π or use 3.14 and enter your answer as a decimal rounded to the nearest hundredth.
Answer:
See Explanation
Explanation:
The question is incomplete as the values of radius and central angle are not given.
However, I'll answer the question using the attached figure.
From the attached figure, the radius is 3 unit and the central angle is 120 degrees
The area of a sector is calculated as thus;
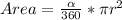
Where
 represents the central angle and r represents the radius
represents the central angle and r represents the radius
By substituting
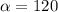 and r = 3
and r = 3
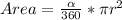 becomes
becomes

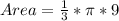
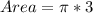
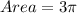 square units
square units
Solving further to leave answer as a decimal; we have to substitute 3.14 for

So,
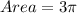 becomes
becomes
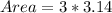
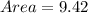 square units
square units
Hence, the area of the sector in the attached figure is
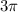 or 9.42 square units
or 9.42 square units