Question

A baseball player hits a ball at an angle of 52 degrees and at a height of 4.5 ft. if the ball's initial velocity after being hit is 152ft/s and if no one catches the ball when will it hit the ground?

Answer 1

`t\approx 5.865\,s`

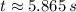
Explanation:

The motion equations that describe the ball are, respectively:

`x = \left[\left(152\,(ft)/(s) \right)\cdot \cos 52^(\circ) \right] \cdot t`

`y = 4.5\,ft + \left[\left(152\,(ft)/(s) \right)\cdot \sin 52^(\circ) \right] \cdot t - (1)/(2)\cdot \left(32.174\,(ft)/(s^(2)) \right) \cdot t^(2)`

The time required for the ball to hit the ground is computed from the second equation. That is to say:

`4.5\,ft + \left[\left(152\,(ft)/(s) \right)\cdot \sin 52^(\circ) \right] \cdot t - (1)/(2)\cdot \left(32.174\,(m)/(s^(2)) \right) \cdot t^(2) = 0`

Given that formula is a second-order polynomial, the roots of the equation are described below:

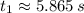`t_(1)\approx 5.865\,s` and
`t_(2) \approx -0.048\,s`

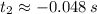
Just the first root offers a realistic solution. Then,
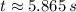`t\approx 5.865\,s`.