Question

What is the complex number z=−3+3√3i represented in polar form?


z=____cis(____)

Answer 1

6cis120°

Explanation:

The general form of a complex number z = x+iy

If x = rcos
`\theta` and y = rsin
`\theta`

where r is the modulus of the complex number and
`\theta` is the argument, z in polar form is represented as:

z = rcos
`\theta`+ rsin
`\theta`

z = r(cos
`\theta`+ isin
`\theta`)

z = rcis
`\theta`

Given the complex number z=−3+3√3i

r =
`\sqrt{x^(2)+y^(2) }`

`r = \sqrt{(-3)^(2)+(3√(3))^(2) } \\r = √(9+27) \\r = √(36)\\ r = 6`

`argument\\\theta = arctan (y)/(x) \\\theta = arctan (3√(3) )/(-3) \\\theta = arctan {-√(3) } \\\theta = -60 \deg`

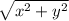
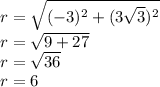
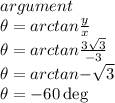
since the argument is negative and tan is negative in the 2nd and 4th quadrant,

In the second quadrant, theta = 180- 60 = 120°

On substituting r and theta, the complex number in polar form is expressed as 6cis120°