Question

Determine the area of a triangle with A=27.8 B = 107.3 c=4


Answer: B) 10 units^2

Answer 1

Correct question:

Determine the area of a triangle with A=27.8° B = 107.3° c=4

Answer:

Area of the triangle is 5.04 units²

Explanation:

Given;

A = 27.8°

B = 107.3°

C = 180 - (27.8 + 107.3) = 44.9°

c = 4

Now, we determine the remaining two sides of the triangle using sine rule

`(Sine \ A)/(a) = (Sine \ C)/(c) \\\\a = (Sine A*\ c)/(Sine C) = (Sine(27.8) \ *4)/(Sine(44.9) ) =2.64\\\\(Sine \ B)/(b) = (Sine \ C)/(c)\\\\b= (Sine B*\ c)/(Sine C) = (Sine(107.3) \ *4)/(Sine(44.9) ) =5.41`

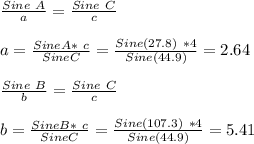
Apply Hero's formula;

`A = √(s(s-a)(s-b)(s-c)) \\\\s = (a+b+c)/(2) = (2.64\ +\ 5.41\ +\ 4)/(2) = 6.025\\\\A = √(6.025(6.025-2.64)(6.025-5.41)(6.025-4)) \\\\A = √(6.025(3.385)(0.615)(2.025)) \\\\A = √(25.3989) = 5.04 \ units^2`

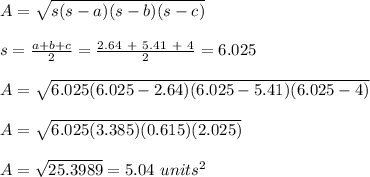
Therefore, area of the triangle is 5.04 units²