Answer:
E = 8991.8 N/C
Step-by-step explanation:
To find the electric flux in the sphere you use the Gaussian formula:
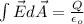
but, electric field is given by
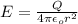
in each point of the sphere surface, electric field is parallel to the normal vector of the surface:
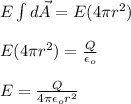
Then, for r = 1.00 m you have:
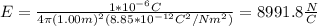
where you have used that εo = 8.85*10^-12 C^2/Nm^2