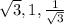Answer:
The common ratio is
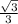 and the next three terms of the sequence are
and the next three terms of the sequence are
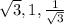
Explanation:
Given the geometric series a1, a2, a3... the common ratio is expressed as;
r = a2/a1 = a3/a2
The nth term of a geometric sequence Tn =

where n is the number of terms
r is the common ratio
Now given the sequence 9,3
 , 3...
, 3...
common ratio

The next three terms are the 4th, 5th and 6th term
To get the 4th term when n = 4
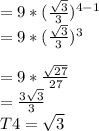
When n= 5
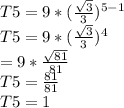
when n = 6
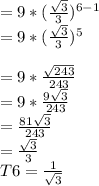
The next three terms of the sequence are