Question

A sporting equipment company wants to sell a new bicycle helmet. They have developed a function, shown below, where total profit, p, can be determined based on sale price, s.

What will be the total profit if the sale price of the helmet is $60?

Answer 1

`p(s) = -24s^2 +2200 s -18000`

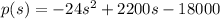
If we use the valie of s =60 we have

`p(60) = -24 (60)^2 +2200*60 -18000`

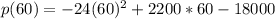
And after solve we got:

`p(60)= -86400 +132000 -18000 =27600`

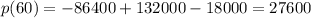
So then the best option for this case would be:

$27,600

Explanation:

Using the following info in order to complete the problem:

p(s)=-24s^(2)+2200s-18000

$112,560

$27,600

$111,120

$236,400

$14,240

We have the following function given:

`p(s) = -24s^2 +2200 s -18000`

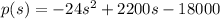
If we use the valie of s =60 we have

`p(60) = -24 (60)^2 +2200*60 -18000`

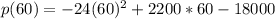
And after solve we got:

`p(60)= -86400 +132000 -18000 =27600`

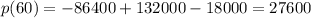
So then the best option for this case would be:

$27,600