Answer:
1. pOH = 1.01 and the pH = 12.99.
2. a) %I = 0.417 %, b) pH = 2.34.
Step-by-step explanation:
1. The pH of the dissolution of Ba(OH)₂ in water can be calculated using the following equation:
![pH = 14 - pOH = 14 - (-log[OH^(-)]) = 14 + log[OH^(-)]](https://img.qammunity.org/2021/formulas/chemistry/middle-school/hs5kanxvausgrho7drlse8t9jwl6gkzg58.png)
To find the pOH, first, we need to calculate the concentration (C) of Ba(OH)₂:
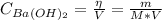
Where:
η: is the number of moles of Ba(OH)₂
V: is the volume of the solution = 100 ml = 0.100 L
M: is the molar mass of Ba(OH)₂ = 171.34 g/mol
m: is the mass of Ba(OH)₂ = 0.837 g
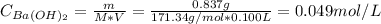
Knowing that in 1 mol of Ba(OH)₂ we have two moles of OH⁻, the concentration of OH⁻ is:
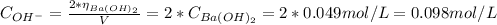
Now, we can find the pOH and the pH of the solution:
![pOH = -log[OH^(-)] = -log(0.098) = 1.01](https://img.qammunity.org/2021/formulas/chemistry/middle-school/lp90uawzzcekzk6rqszab8sddxojioe0s1.png)
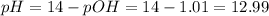
2. a) The percentage of ionization (% I) of acetic acid can be calculated using the following equation:
![\% I = ([H^(+)]_(eq))/([HA]_(0))*100](https://img.qammunity.org/2021/formulas/chemistry/middle-school/bwkazfxusp9a7wxwue0vi98jr8swjqq29f.png)
We need to find the [H⁺] = [H₃O⁺] at the equilibrium:
CH₃COOH(aq) + H₂O(l) → CH₃COO⁻(aq) + H₃O⁺(aq)
1.0 - x x x
![Ka = ([CH_(3)COO^(-)]*[H_(3)O^(+)])/([CH_(3)COOH])](https://img.qammunity.org/2021/formulas/chemistry/middle-school/55lj3ymbygnn3duov1xxq24nch64qmfny7.png)
Ka: is the dissociation constant of acetic acid = 1.75x10⁻⁵
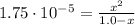
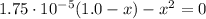 (1)
(1)
By solving equation (1) for x we have two solutions:
x₁ = -0.00417
x₂ = 0.00417 = [H₃O⁺] = [CH₃COO⁻]
We will take the positive value to find the percentage ionization:
![\% I = ([H^(+)]_(eq))/([HA]_(0))*100 = (0.00417 M)/(1.0 M)*100 = 0.417 \%](https://img.qammunity.org/2021/formulas/chemistry/middle-school/bzdal3lxihpqli65klcd913t5jqojyra5c.png)
b) The pH of the solution is:
![pH = -log([H_(3)O^(+)]) = -log(0.00417) = 2.34](https://img.qammunity.org/2021/formulas/chemistry/middle-school/hj7ye4ml4861n2k6oq7f4qd4c3x2unblln.png)
I hope it helps you!