Answer:
 (1)
(1)
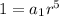 (2)
(2)
If we divide equations (2) and (1) we got:
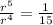
And then
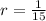
And then we can find the value
 and we got from equation (1)
and we got from equation (1)
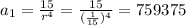
And then the general term for the sequence would be given by:

And the best option would be:
C) a1=759,375; an=an−1⋅(1/15)
Explanation:
the general formula for a geometric sequence is given by:
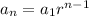
For this case we know that
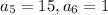
Then we have the following conditions:
 (1)
(1)
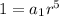 (2)
(2)
If we divide equations (2) and (1) we got:
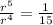
And then
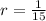
And then we can find the value
 and we got from equation (1)
and we got from equation (1)
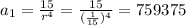
And then the general term for the sequence would be given by:

And the best option would be:
C) a1=759,375; an=an−1⋅(1/15)