Answer:
1)
 , 2)
, 2)
 , 3)
, 3)
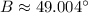 , 4)
, 4)
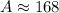 , 5) Unsolvable due to lack of information.
, 5) Unsolvable due to lack of information.
Explanation:
1) The angle B is determined by the Law of Sines:
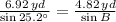
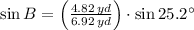
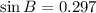

The angle C is:
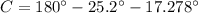

2) The side c is computed by the Law of Cosine:
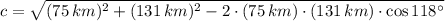

3) The angle B is determined with the help of the Law of Cosine:
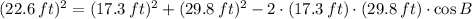
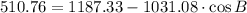
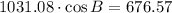
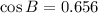
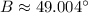
4) The formula for the surface of a triangle by just knowing their sides is:
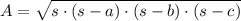 , where
, where
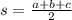 .
.
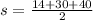
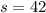
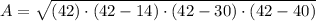
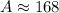
5) The statement is not complete and there is no possibility to find the figure).