We are asked to find the probability that a data value in a normal distribution is between a z-score of -1.32 and a z-score of -0.34.
The probability of a data score between two z-scores is given by formula
 .
.
Using above formula, we will get:
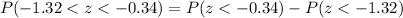
Now we will use normal distribution table to find probability corresponding to both z-scores as:
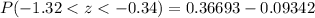
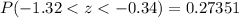
Now we will convert
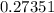 into percentage as:
into percentage as:
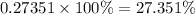
Upon rounding to nearest tenth of percent, we will get:
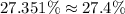
Therefore, our required probability is 27.4% and option C is the correct choice.