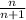Answer:
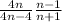
We can take common factor of 4 for the term
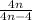 and we got:
and we got:
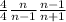
Now we can cancel the n-1 in the denominator and the n-1 in the numerator and we got:
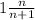
And the final answer would be:
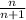
Explanation:
For this case we have the following product given:
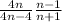
We can take common factor of 4 for the term
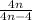 and we got:
and we got:
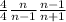
Now we can cancel the n-1 in the denominator and the n-1 in the numerator and we got:
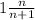
And the final answer would be: