Question

1. The number of employees at a certain company is 1440 and is increasing

at a rate of 1.5% per year. Write an exponential growth function to model

this situation. Then find the number of employees in the company after 9

years.

Answer 1

`y = 1440 e^(0.015 t)`

`y(9) = 1440 e^(0.015*9)= 1648.133`

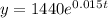
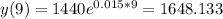
So then after 9 years we will have approximately 1649 number of employees

Explanation:

For this case we want to model the number of employees and we need to use an exponential model given by this general expression:

`y = y_o e^(rt)`

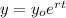
For this case the initial amount is
`y_o = 1440` and the rate
`r =0.015`

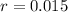
And then the model would be given by

`y = 1440 e^(0.015 t)`

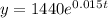
And if we find the value for t =9 years we got:

`y(9) = 1440 e^(0.015*9)= 1648.133`

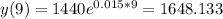
So then after 9 years we will have approximately 1649 number of employees