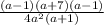Question

Perform the indicated operation and simplify your answer in factored form.

a^2+6a-7/2a^2+4a^2+2a*2a/a^2-1

Answer 1

`((a-1)(a+7)(a-1))/(4a^(2)(a+1) )`

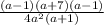
Explanation:

The given expression is

`((a^(2) +6a-7))/(((2a^(3) +4a^(2) +2a)(2a))/((a^(2) -1)) )`

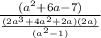
First, we solve the division

`((a^(2) -1)(a^(2) +6a-7))/((2a^(3) +4a^(2) +2a)(2a))`

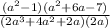
Second, we factor the numerator

`(a^(2) -1)(a^(2) +6a-7)=(a+1)(a-1)(a+7)(a-1)`

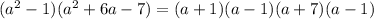
The first expression is the difference between two perfect squares, and the second expression is about finding to number which product is 7 and which difference is 6.

Third, we factor the denominator

`(2a^(3) +4a^(2) +2a)(2a)`

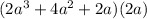
We extract the common factor from the trinomial

`2a(a^(2)+2a+1 )(2a)=4a^(2)(a^(2)+2a+1 )`

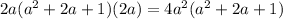
Now, we find two number which product is 1 and which sum is 2

`4a^(2)(a^(2)+2a+1 )=4a^(2)(a+1)(a+1)`

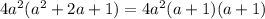
Then, we replace all factor in the initial fraction

`((a+1)(a-1)(a+7)(a-1))/(4a^(2)(a+1)(a+1) )`

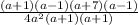
Equal factors are simplified, given as result

`((a-1)(a+7)(a-1))/(4a^(2)(a+1) )`

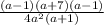
Therefore, the answer in factored form is

`((a-1)(a+7)(a-1))/(4a^(2)(a+1) )`