Question

Pascal wanted the area of the floor to be 54 ft.² in the word still to be 2/3 the lake what was the demons

Answer 1

The dimensions of the floor are 9 feet length and 6 feet width.

Explanation:

The complete question is

Pascal wanted the area of the floor to be 54 square feet and the width still to be 2/3 the length?what would the dimensions of the floor be.

We know that the area of a rectanlge is
`A= w * l`, where
`w` is width and
`l` is length.

Now, according to the problem, the width is 2/3 of the length, that means

`w=(2)/(3)l`

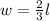
And the area is
`A=54 \ ft^(2)`, replacing them, we have

`54=(2)/(3)l * l`

Then, we solve for the length

`54=(2)/(3)l^(2)\\ (162)/(2)=l^(2) \\ l^(2) =81\\l=√(81)=9`

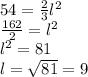
So, the length of the floor is 9 feet long.

Now, we use the length value to find the width

`w=(2)/(3)(9)=6`

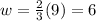
So, the width is 6 feet long.

Therefore, the dimensions of the floor are 9 feet length and 6 feet width.