Question

1500 customers hold a VISA card; 500 hold an American Express card; and, 75 hold a VISA and an American Express. What is the probability that a customer chosen at random holds a VISA card, given that the customer has an American Express card?

Answer 1

There is 15% probability that a customer chosen at random holds a VISA card, given that the customer has an American Express card.

`P(VISA \:| \:AE) = 15\%\\`

Explanation:

Number of customers having a Visa card = 1,500

Number of customers having an American Express card = 500

Number of customers having Visa and American Express card = 75

Total number of customers = 1,500 + 500 = 2,000

We are asked to find the probability that a customer chosen at random holds a VISA card, given that the customer has an American Express card.

This problem is related to conditional probability which is given by

`P(A \:| \:B) = (P(A \:and \:B))/(P(B))`

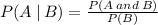
For the given problem it becomes

`P(VISA \:| \:AE) = (P(VISA \:and \:AE))/(P(AE))`

The probability P(VISA and AE) is given by

P(VISA and AE) = 75/2000

P(VISA and AE) = 0.0375

The probability P(AE) is given by

P(AE) = 500/2000

P(AE) = 0.25

Finally,

`P(VISA \:| \:AE) = (P(VISA \:and \:AE))/(P(AE))\\\\P(VISA \:| \:AE) = (0.0375)/(0.25)\\\\P(VISA \:| \:AE) = 0.15\\\\P(VISA \:| \:AE) = 15\%\\`

Therefore, there is 15% probability that a customer chosen at random holds a VISA card, given that the customer has an American Express card.