Answer:
(D)$81
Explanation:
Given that the number of purses a vendor sells daily has the probability distribution represented in the table.
Expected Value,
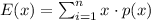
Therefore:
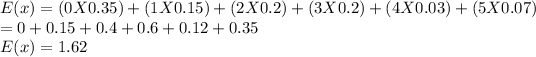
If each purse sells for $50.00, the number of expected daily total dollar amount taken in by the vendor from the sale of purses
=Expected Value X $50
=1.62 X $50
=$81
The correct option is D.