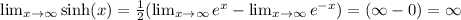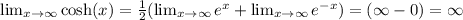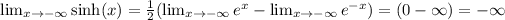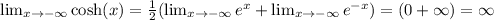Question

The Hyperbolic Sine (sinh(x)) and Hyperbolic Cosine (cosh(x)) functions are defined as such: sin h(x) = e^x - e^-x/2 cosh(x) = e^x + e^-x/2 Compute the y-Intercept of both functions Then Determine the end behavior of these two functions by analyzing the limit as x goes to positive infinity and as x goes to negative infinity

Answer 1

y-incercepts:

sinh(x):0, cosh(x)=1

Limits:

positive infinity: sinh(x): infinity, cosh(x): infinity

negative infinity: sinh(x): - infinity, cosh(x): infinity

Explanation:

We are given that

`\sinh(x)=(e^(x)-e^(-x))/(2)`

`\cosh(x)=(e^(x)+e^(-x))/(2)`

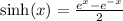
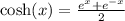
To find out the y-incerpt of a function, we just need to replace x by 0. Recall that
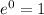`e^(0)=1`. Then,

`\sinh(0) = (1-1)/(2)=0`

`\cosh(0) = (1+1)/(2)=1`

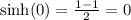
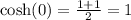
For the end behavior, recall the following:

`\lim_(x\to \infty)e^(x) = \infty, \lim_(x\to \infty)e^(-x) = 0`

`\lim_(x\to -\infty)e^(x) = 0, \lim_(x\to -\infty)e^(-x) = \infty`

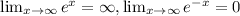
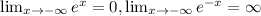
Using the properties of limits, we have that

`\lim_(x\to \infty) \sinh(x) =(1)/(2)(\lim_(x\to \infty)e^(x)-\lim_(x\to \infty)e^(-x))=(\infty -0) = \infty`

`\lim_(x\to \infty) \cosh(x) =(1)/(2)(\lim_(x\to \infty)e^(x)+\lim_(x\to \infty)e^(-x)) =(\infty -0)= \infty`

`\lim_(x\to -\infty) \sinh(x) =(1)/(2)(\lim_(x\to -\infty)e^(x)-\lim_(x\to -\infty)e^(-x)) = (0-\infty)=-\infty`

`\lim_(x\to -\infty) \cosh(x) =(1)/(2)(\lim_(x\to -\infty)e^(x)+\lim_(x\to -\infty)e^(-x)) =(0+\infty)= \infty`